手算开平方的方法其实有很多，我先来教大家一种连分数的方法。如果要计算一个数s的平方根，只需要把这个数写成s=a²+b （a²>>b）的形式，然后就可以通过下面的式子计算：
$$\sqrt{S}=a+\dfrac{b}{2a+\dfrac{b}{2a+\ldots }}\left( 1\right)$$

观察这个式子，你会发现：除了第一项是a，其余的加号前面都是2a，分子都是b，很好记。这个连分数有无限多层，但是我们在计算过程中不需要取无限多层，只需要一两层，就能得到很好的效果。

比如，我们要计算150的平方根。我们将150写成144+6，前者是12的平方，即150=12²+6，也就是在（1）式中a=12，b=6

我们可以按照不同的精度，分别取0层、1层、2层…近似
$$\sqrt{s}\approx a=12\left( 0层近似\right)$$
$$\sqrt{s}\approx a+\dfrac{b}{2a}=12+\dfrac{6}{24}=12.25\left( 1层近似\right)$$
$$\sqrt{s}\approx a+\dfrac{b}{2a+\dfrac{b}{2a}}=12+\dfrac{6}{24+\dfrac{6}{24}}=12.2474\left( 2层近似\right)$$

如果我们用计算机按出根号150，它等于12.2474487…，大家会发现，其实1层近似就已经很准确了，到了2层近似的时候，已经准确到小数点后第四位了，误差在百万分之二，怎么样？还是很不错的方法吧！ 

这种方法的证明也不难。如下：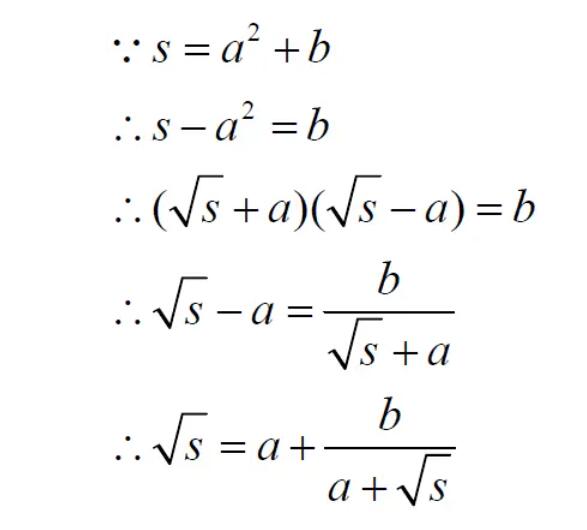

大家观察最后一个表达式：左右两侧都等于√s，而在右侧表达式的右下角还有√s。于是，我们可以把右侧整个代入到右下角的√s中。

这样就得到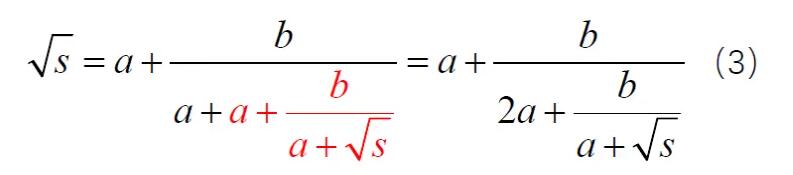

大家看，这样就出现了一个2a。我们可以重复这个步骤，用（2）中的绿色框再次替代（3）中右下角的√s，这样就得到了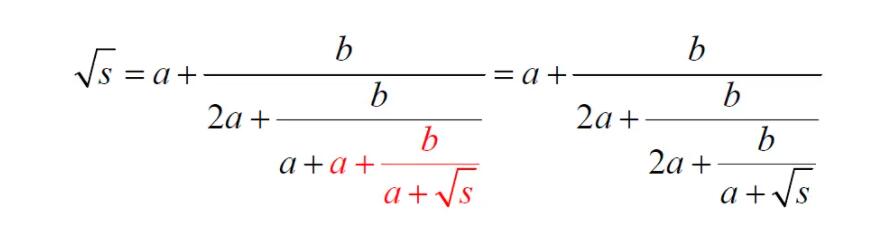

如此，我们反反复复计算下去，就会得到最初的结论（1）了。怎么样？简单吧!

作者：李永乐老师官方